PageRank Measures the Wrong Fixed Point Under Polarization

Directly evaluating information quality at web scale is intractable. Early web search adopted PageRank¹ as a scalable surrogate: rather than grade content, infer a site's credibility; rather than measure credibility directly, use inter-site links as votes. The chain—quality ← credibility ← links—stacks two proxies. It works when the behavior behind links approximates cross-cutting endorsement.
Those proxies bake in assumptions: links are mostly endorsements rather than attacks or reciprocal favors; incentives to link are not dominated by in-group loyalty or coordination; and there is sufficient cross-cutting connectivity for endorsement to percolate. When those assumptions fail, the proxy decouples from the target.
What polarization does to random-walk scores
Personalized PageRank and related centralities are diffusion processes. They concentrate probability mass in low-conductance regions—parts of the graph with few edges going out. Polarization creates exactly such regions: camps with dense internal links and few bridges. As conductance between camps falls, random walks get bottlenecked and PageRank becomes a local centrality, ranking leaders inside each camp rather than sources with broad, cross-cutting credibility. Community detection literature² treats this "localization" as a feature; for credibility estimation, it is a failure mode.
A compact model that makes the failure explicit
Split publishers into two camps $A$ and $B$. An outlink from $i$ to $j$ follows a mixed motive:
$$\Pr(i \to j) \propto (1 - \theta) \cdot \exp(\beta \cdot q_j) + \theta \cdot \mathbf{1}{g_i = g_j}$$
Here $q_j$ is camp-agnostic source quality; $g_i \in {A, B}$ is $i$'s camp; $\beta \geq 0$ controls attention to quality; $\theta \in [0, 1]$ indexes polarization (homophily). PageRank $p$ solves the usual fixed point with teleport $\alpha \in (0, 1)$.
Let $\phi$ be the conductance of the cut between $A$ and $B$ (formally: the minimum probability of exiting a camp in one step, normalized by that camp's stationary mass). Cheeger-type arguments³ imply a localization statement: as $\phi \to 0$,
$$p \approx w_A \cdot p^{(A)} \oplus w_B \cdot p^{(B)} + O\left(\frac{\phi}{\alpha + \phi}\right)$$
So the global correlation between PageRank $p$ and true quality $q$ collapses to a weighted average of within-camp correlations plus a vanishing bridge term. If within each camp links weakly encode quality (small $\beta$), then $\text{Corr}(p, q) \to 0$ even when $\text{Var}(q) > 0$.
Intuition: The random walk gets trapped inside camps; PageRank becomes a camp-popularity statistic rather than a cross-camp credibility signal.
Empirical preconditions and implications
Modern political link and resharing graphs exhibit high assortativity⁴⁵⁶: liberals mostly link to liberals; conservatives to conservatives; cross-exposure is limited. Under those conditions, the prerequisites for PageRank's credibility failure are satisfied by construction.
The practical upshot is predictable:
- The "authoritative sources" list bifurcates, each camp crowning its own authorities
- Minority or cross-cutting outlets are under-ranked regardless of factual reliability
- Algorithm outputs reinforce rather than bridge polarization
Why tweaks won't rescue credibility
Signed variants (trust/distrust propagation⁷) help only when we reliably observe which links are endorsements versus attacks or when we possess dense, unbiased seeds—both rare under polarization.
Fairness-aware reweighting can constrain representation but changes the objective from credibility estimation to allocation.
None of these alter the underlying diffusion physics: with scarce bridges, random walks still localize.
What to do instead
If the graph lacks a cross-camp endorsement signal, link-based centrality is the wrong primitive. Credibility estimation must inject exogenous evidence:
- Outcome-grounded audits: fact-check concordance, correction records
- Byline-level track records: individual journalist accuracy over time
- Topic-calibrated error rates: performance on verifiable predictions
- Supervised models: treat links as one weak feature among many
- Lean on expert browsers: learn from the choices of expert browsers
In other words, interpret PageRank as community authority when polarization is high, and seek credibility off-graph.
Appendix A: Sketch of the localization bound
Let $G$ be a strongly connected directed graph with transition matrix $P$ and teleport parameter $\alpha$. For seed distribution $u$, PageRank is $p = \alpha u + (1 - \alpha)P^T p$.
Partition $V$ into camps $A, B$ with conductance $\phi = \min{\Phi(A), \Phi(B)}$, where $\Phi(S)$ is the probability (under the PageRank random walk) of exiting $S$ in one step divided by the stationary mass of $S$.
Then there exist weights $w_A, w_B$ and within-camp PageRank vectors $p^{(A)}, p^{(B)}$ such that:
$$|p - (w_A p^{(A)} \oplus w_B p^{(B)})|_1 \leq C \cdot \frac{\phi}{\alpha + \phi}$$
for some absolute constant $C$.
Proof sketch:
- Express PageRank in resolvent form: $p = \alpha(I - (1-\alpha)P^T)^{-1}u$
- Decompose paths by number of boundary crossings using inclusion-exclusion
- Apply conductance bounds showing $k$-crossing paths contribute $O(\phi^k)$
- Sum geometric series to obtain $O(\phi/(\alpha+\phi))$ total cross-camp contribution
This yields the mixture approximation: when $\phi$ is small relative to $\alpha$, teleportation is far likelier to keep the walk within its current camp than edges are to carry it across.
Appendix B: Toy Experiment
Goal: Demonstrate that as polarization increases (fewer cross-camp links), PageRank ceases to track global source quality and instead reflects within-camp popularity.
Setup:
- $n = 200$ publishers split evenly into two camps
- Each publisher $j$ has camp-agnostic quality $q_j \sim \mathcal{N}(0, 1)$
- Generate outlinks via mixed-motive rule
- Compute PageRank with teleport $\alpha = 0.15$ and uniform teleport vector
- Vary $\theta$ from 0 (quality-focused links) to 0.98 (camp-focused links)
Metrics:
- Global correlation $\text{Corr}(p, q)$
- Within-camp correlations
- Approximate conductance (average one-step cross-camp probability)
- Overlap between top-10 by PageRank vs. top-10 by quality
Results (this run, seed = 7). As polarization increases, the cross‑camp step mass falls sharply. Over the same range, the global PageRank–quality correlation declines, while within‑camp correlations remain relatively flat. At high polarization (e.g., θ ≈ 0.95), the top‑10 lists by PageRank vs. true quality still overlap within camps, but PageRank is visibly less aligned with quality globally. Lowering the quality weight (e.g., β = 0.25) makes the collapse more pronounced: global alignment falls further, and top‑k overlap deteriorates.
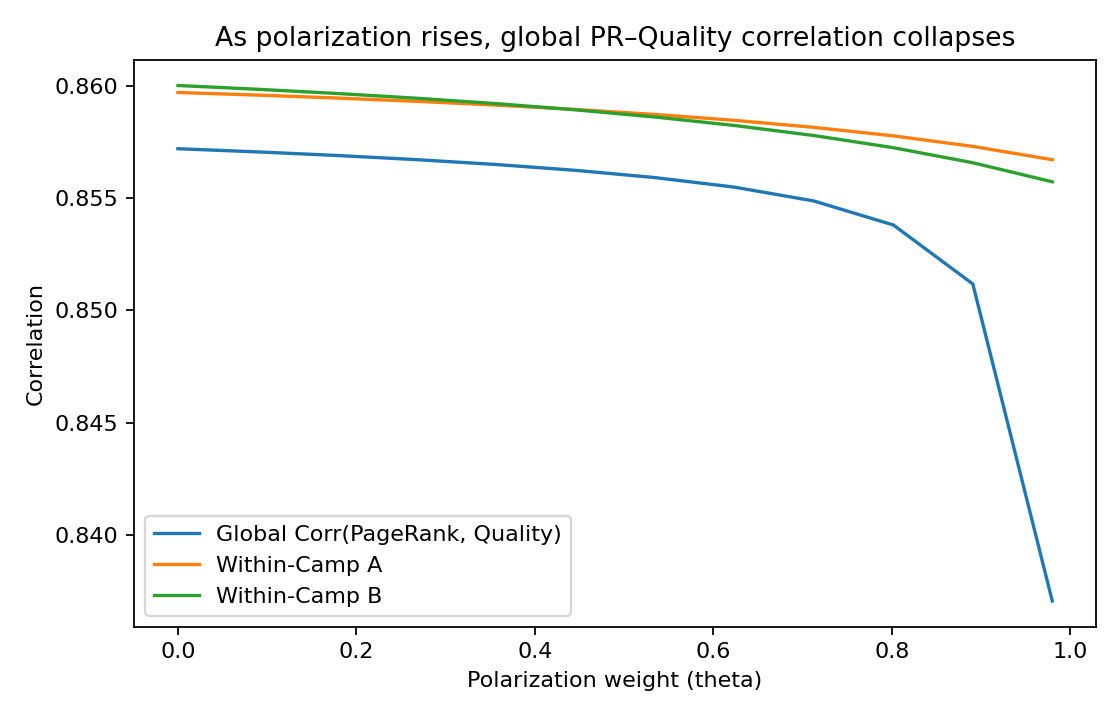
Interpretation. The random‑walk mass increasingly localizes in low‑conductance communities as bridges disappear. Teleportation prevents total trapping but does not restore the cross‑camp endorsement signal. PageRank thus transitions from a cross‑community credibility proxy to a camp‑authority score.
Implementation notes. The demo uses a dense transition matrix — an “infinite‑sample” view of the link mechanism — to avoid Monte‑Carlo noise; results are qualitatively unchanged if we sample a sparse directed multigraph. Self‑links are disabled; the teleport vector is uniform (no personalization). The code and plot are available in the shared artifacts for this project.
# Polarization vs. PageRank-as-Credibility: a tiny, runnable demo
#
# What this does:
# 1) Simulates a 2-camp publishing graph where links are driven by a mix of quality and polarization.
# 2) Computes PageRank of the resulting Markov chain (with teleportation).
# 3) Shows how the global correlation between PageRank and true quality collapses as polarization rises,
# while within-camp correlations remain small and relatively flat.
# 4) Prints a concrete snapshot at high polarization: top-by-PageRank vs. top-by-quality.
#
# You can re-run with different seeds/params to play. Outputs include a CSV and a PNG you can download.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from math import isfinite
# -----------------------------
# Utilities
# -----------------------------
def pagerank_from_transition(T, alpha=0.15, tol=1e-12, max_iter=10000):
"""
Compute PageRank vector p for a given row-stochastic transition matrix T:
p = alpha * u + (1-alpha) * p T
where u is uniform.
Returns p as a 1D numpy array of length n (sum(p)=1).
"""
n = T.shape[0]
u = np.ones(n) / n
p = u.copy()
for _ in range(max_iter):
p_new = alpha * u + (1 - alpha) * (p @ T)
if np.linalg.norm(p_new - p, ord=1) < tol:
p = p_new
break
p = p_new
# Ensure normalization
p = p / p.sum()
return p
def build_transition_matrix(q, camps, theta=0.8, beta=1.0):
"""
Build a dense row-stochastic transition matrix T given:
- q: quality vector (higher means more likely link under "quality motive")
- camps: array of camp labels (e.g., 0 or 1) per node
- theta: polarization weight in [0,1]; 1 => pure homophily, 0 => pure quality-seeking
- beta: strength of quality preference in the mixed motive
Transition probabilities from i to j are proportional to:
(1-theta)*exp(beta*q_j) + theta*1[camp_i == camp_j]
Self-links are zeroed before normalization.
"""
n = len(q)
Q = np.exp(beta * q) # quality attractiveness
T = np.zeros((n, n), dtype=float)
for i in range(n):
same = (camps == camps[i]).astype(float)
w = (1 - theta) * Q + theta * same
w[i] = 0.0 # no self-link
s = w.sum()
if s <= 0:
# Fallback to uniform if pathological (shouldn't happen with the mix above)
T[i, :] = 1.0 / (n - 1)
T[i, i] = 0.0
else:
T[i, :] = w / s
return T
def cross_edge_mass(T, camps):
"""
Average probability of crossing between camps in one step (A->B and B->A averaged).
"""
n = len(camps)
camps = np.asarray(camps)
A = np.where(camps == camps[0])[0] # all nodes with same label as first
# In case labels are not 0/1, get unique camps
labels = np.unique(camps)
if len(labels) != 2:
# Generalize to two largest groups if more than 2 labels exist
counts = [(lab, np.sum(camps == lab)) for lab in labels]
counts.sort(key=lambda x: -x[1])
labA, labB = counts[0][0], counts[1][0]
A = np.where(camps == labA)[0]
B = np.where(camps == labB)[0]
else:
labA, labB = labels[0], labels[1]
A = np.where(camps == labA)[0]
B = np.where(camps == labB)[0]
mass_A_to_B = T[A][:, B].sum() / len(A)
mass_B_to_A = T[B][:, A].sum() / len(B)
return 0.5 * (mass_A_to_B + mass_B_to_A)
# -----------------------------
# Experiment
# -----------------------------
rng = np.random.default_rng(7) # reproducible but tunable seed
n = 200 # total nodes
beta = 1.0 # strength of quality-seeking
alpha = 0.15 # teleport
# Split into two equal camps
camps = np.array([0] * (n // 2) + [1] * (n - n // 2))
# True quality signal (camp-agnostic)
q = rng.normal(0.0, 1.0, size=n)
thetas = np.linspace(0.0, 0.98, 12) # from no polarization to strong polarization
rows = []
for theta in thetas:
T = build_transition_matrix(q, camps, theta=theta, beta=beta)
p = pagerank_from_transition(T, alpha=alpha, tol=1e-12, max_iter=10000)
# Correlations
corr_global = np.corrcoef(p, q)[0, 1]
A = (camps == 0)
B = ~A
corr_A = np.corrcoef(p[A], q[A])[0, 1]
corr_B = np.corrcoef(p[B], q[B])[0, 1]
xmass = cross_edge_mass(T, camps)
# Rank percentile of the best-quality node
best = np.argmax(q)
rank = np.argsort(-p) # indices sorted by descending PR
rank_pos = int(np.where(rank == best)[0][0]) + 1 # 1-based
top_percentile = 1.0 - (rank_pos - 1) / n
rows.append({
"theta_polarization": theta,
"cross_edge_mass": xmass,
"corr_global_PR_vs_quality": corr_global,
"corr_within_A": corr_A,
"corr_within_B": corr_B,
"best_quality_node_rank_percentile": top_percentile
})
df = pd.DataFrame(rows)
# Clean any possible numerical noise (NaNs from degenerate cases)
for c in ["corr_global_PR_vs_quality", "corr_within_A", "corr_within_B"]:
df[c] = df[c].apply(lambda x: float(x) if isfinite(x) else np.nan)
# Save CSV
csv_path = "pagerank_polarization_results.csv"
df.to_csv(csv_path, index=False)
# Plot correlation vs. polarization
plt.figure(figsize=(7, 4.5))
plt.plot(df["theta_polarization"], df["corr_global_PR_vs_quality"], label="Global Corr(PageRank, Quality)")
plt.plot(df["theta_polarization"], df["corr_within_A"], label="Within-Camp A")
plt.plot(df["theta_polarization"], df["corr_within_B"], label="Within-Camp B")
plt.xlabel("Polarization weight (theta)")
plt.ylabel("Correlation")
plt.title("As polarization rises, global PR–Quality correlation collapses")
plt.legend()
png_path = "pagerank_polarization_correlation.png"
plt.tight_layout()
plt.savefig(png_path, dpi=160)
plt.show()
# Snapshot at high polarization
theta_demo = 0.95
T_demo = build_transition_matrix(q, camps, theta=theta_demo, beta=beta)
p_demo = pagerank_from_transition(T_demo, alpha=alpha)
# Top by PageRank vs. Top by Quality
k = 10
top_pr_idx = np.argsort(-p_demo)[:k]
top_q_idx = np.argsort(-q)[:k]
def summarize(indices):
return pd.DataFrame({
"node": indices,
"camp": camps[indices],
"true_quality": q[indices],
"pagerank": p_demo[indices]
}).reset_index(drop=True)
top_pr_df = summarize(top_pr_idx)
top_q_df = summarize(top_q_idx)
print("Polarization demo: top-10 by PageRank (theta=0.95)")
print(top_pr_df)
print("Polarization demo: top-10 by True Quality (theta=0.95)")
print(top_q_df)
csv_top_pr = "top10_by_pagerank_theta095.csv"
csv_top_q = "top10_by_quality.csv"
top_pr_df.to_csv(csv_top_pr, index=False)
top_q_df.to_csv(csv_top_q, index=False)
png_path, csv_path, csv_top_pr, csv_top_q
References
- Page, L., Brin, S., Motwani, R., & Winograd, T. (1998). The PageRank citation ranking: Bringing order to the web. Stanford InfoLab Technical Report.
- Fortunato, S. (2010). Community detection in graphs. Physics Reports, 486(3-5), 75-174.
- Chung, F. (1997). Spectral Graph Theory. American Mathematical Society.
- Adamic, L. A., & Glance, N. (2005). The political blogosphere and the 2004 U.S. election. Proceedings of LinkKDD.
- Conover, M., Ratkiewicz, J., Francisco, M., Gonçalves, B., Menczer, F., & Flammini, A. (2011). Political polarization on Twitter. Proceedings of ICWSM.
- Bakshy, E., Messing, S., & Adamic, L. A. (2015). Exposure to ideologically diverse news and opinion on Facebook. Science, 348(6239), 1130-1132.
- Guha, R., Kumar, R., Raghavan, P., & Tomkins, A. (2004). Propagation of trust and distrust. Proceedings of WWW, 403-412.